n個の中からr個を選んで、順番に並べたときの並べ方の総数を計算します。

全体の数(n個)と選んだ数(r個)を入力し「順列を計算」ボタンをクリックすると、n個の中から重複しないでr個を選んで、順番に並べたときの並べ方の総数を計算して表示します。

また、並べ方の総数を求める計算方法も表示します。

全体の数と選んだ数は10,000までの正の整数で入力してください。

順列とは、区別可能な異なるものの中からいくつかを選んで、並べた列のことです。

順列の並べ方の総数は、_nP_rと書いて、全体の数(n個)から選んだ数(r個)の並べ方の総数を表します。

例えば、A、B、Cの3つのアルファベットを並べるとします。

並べ方を樹形図で描くと以下のようになります。

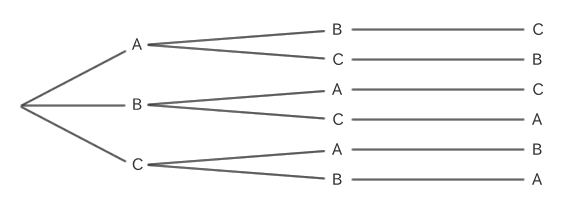
このときの並べ方は、「ABC、ACB、BAC、BCA、CAB、CBA」の6通りになります。

順列では、順番に並べるので並び方が異なる場合は違うものとして考えます。

順列で並べ方の総数を計算する場合、樹形図のように一番目に並ぶのは何通りあるか、二番目に並ぶのは何通りあるかと考えていきます。

例えば、A、B、C、Dの4つのアルファベットがあり、この中から3つを選んで並べるとします。

一番目はA、B、C、Dの4通り、二番目は一番目以外の3通り、三番目は2通りと減っていきます。

よって、並べ方の総数は4×3×2で24通りになります。

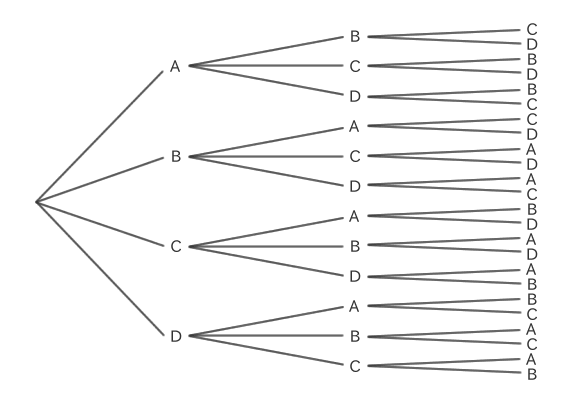
このように、全体の数(n個)から選んだ数(r個)の並べ方の総数は、n、(n−1)、(n−2)と掛けていきそれがr個並びます。

並べ方の総数 = n × (n−1) × (n−2) × ... × (n−r+1)

よって、階乗を使って順列の公式を表すと以下のようになります。